以前、こちらの記事を執筆した際、今後30年間にわたり毎月20万円を積立投資した場合の信託報酬総額を計算しました。
今回は、これに関連し、エクセルを用いて将来の資産額を計算する方法について解説します。
FV関数をマスターしよう
野村証券のウェブサイトによれば、現在価値とは次のように説明できます。
将来の価値から金利などを割り引くことにより、いま手にした場合の価値を導き出すという考え方を現在価値という。
金融商品を購入検討する際に、現在価値を算定し、実際の価格と比較することも必要である。算出された現在価値と実際の価格を比較するなど、投資を検討する際に用いられる。
例えば、1年後に100万円を手にできるとして、金利を1%とした場合、税金や手数料などを考慮しないで計算をする。と、
理論上の現在価値は約990,099円(=100万円÷1.01)となる。
仮に実際の価格が990,000円であった場合、
比較をすると、理論価値より実際の価格の方が安いので、購入するには、割安であるといえる。このように、将来の価値から金利などを割り引くことにより、いま手にした場合の価値を導き出すという考え方を現在価値という。
(出典:野村証券「証券用語解説集」)
インデックス投資においては、将来のある時点における資産保有額を想定利回りで割り引いた現在の価値と言い換えることができます。
この計算を可能にするのがFV(Fair Value)関数です。
具体例で説明します。
・ 月額積立額20万円(年額240万円)
・ 積立期間30年
・ 利回り5.00%
計算の便宜上、毎月20万円ではなく、年始に240万円を投資した場合の計算となります。ご了承ください。検証の内容に影響はありません。

入力する内容は以下のとおりです。
| 項目 | 入力内容 |
| 利率 | 利回りを入力します |
| 期間 | 積立期間を入力します |
| 定期支払額 | 毎期積立金額を入力します |
| 現在価値 | この場合、0を入力します(当初元本がないため) |
| 支払期日 | この場合、1を入力します(1とすると期首積立となり、1年目から複利計算となるため) |
画像のエクセルでは、すでに組み込んだ表があるため、それぞれのセルを参照しています。
結果は以下のとおりです。
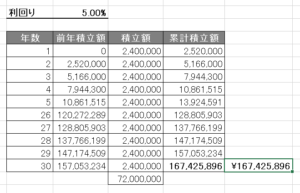
既に組み込んである表の累計積立額と金額が一致していますので、計算結果が正しいことが分かりますね。
FV関数により、毎月20万円を30年間積立投資した場合、5%の利回りで1億6,700万円になることが分かりました。元本が7,200万円なので、複利の効果を実感できますね。
ついでにPMT関数もマスターしよう
現在価値を求めるPV関数に対し、PMT(Payment)関数は、想定利回り下において、ある一定時点の資産残高を達成するための毎期積立額を計算する際に用います。

入力する内容は以下のとおりです。今回は、FV関数で求めた167,425,896円を目標値とします。
| 項目 | 入力内容 |
| 利率 | 利回りを入力します |
| 期間 | 積立期間を入力します |
| 現在価値 | この場合、0を入力します(当初元本がないため) |
| 将来価値 | 将来の目標値を入力します |
| 支払期日 | この場合、1を入力します(1とすると期首積立となり、1年目から複利計算となるため) |
画像のエクセルでは、すでに組み込んだ表があるため、それぞれのセルを参照しています。
結果は以下のとおりです。
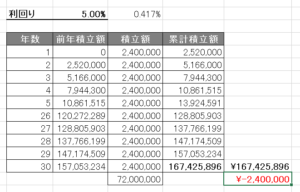
FV関数で求めた金額を得るための毎期積立額が2,400,000万円となるため、計算結果が正しいことが分かりますね。
FV関数により、5%の利回りで30年間積立投資した場合、1億6,700万円を得るためには、毎期240万円の投資が必要になることが分かりました。
これを応用することで、例えば「〇%の利回りで△年投資した場合に、1億円の資産を達成するには、毎月□□円の積立が必要」ということが可能になります。
まとめ
今回は、エクセルを使った現在価値及び毎期積立額の求め方について確認しました。
これらの関数を使えば、将来の資産予想や目標値に対して必要な積立額が明らかになります。インデックス投資期間は長期にわたりますので、早い段階からその時点での正確な予測を行い、都度アップデートすることで、限りなく現状と目標が乖離しないようメンテナンスを行うことが大事だと考えます。






















